学生の研究紹介
指導した修士の学生にやってもらった研究を幾つか紹介します。
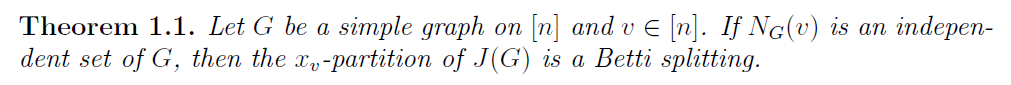
5次元多面体の頂点と辺の数
与えられた自然数の組(v,e)に対して, 頂点の数がvで辺の本数がeの凸多面体が作れますか？というのは多面体についての素朴なな問題です。3次元凸多面体の場合はシュタイニッツが1906年に、4次元の場合はGrunbaumが1967年に答えを出しています。じゃあ5次元ではどうなりますか？という問題を学生さんに考えてもらいました。完全な答えを見つけるのは難しいだろうと思っていたのですが、学生さんがよく考えてくれて、完全な解答を見つけてくれました。
証明は場合分けで、めんどくさい箇所もあるのですが、下のような4次元多面体の絵（シュレーゲル図）を書いて、この形の面ががこっちと張り付くとか、こういう形の面が足りないとかを幾何的に議論する証明で、とても楽しい証明で、また、4次元多面体の絵が描けることをよく使っている証明で感心しました。
この結果は Annals of Combinatorics という雑誌に掲載されました。出版まで時間がかかってしまったので、卒業した学生さんの連絡先がわからず出版されたことの報告が出来ませんでした。Kさんごめんなさい。
面の個数が単峰でない多面体
数列 \(a_1,a_2,…,a_m\) が次の条件を満たすときに単峰であるといいます：
$$a_1 \leq a_2 \leq \cdots \leq a_k \geq \cdots \geq a_m \ \ (\exists k)$$凸多面体を考えるとき, 0次元面の個数, 1次元面の個数, 2次元面の個数, 3次元面の個数…. と順番に並べてできる数列が単峰になるか？というのはかなり昔から考えられていた問題のようです。結局、この問題には反例があることがわかっていて、Zieglerの第8.6章に色々な例が説明されています。
Zieglerの本に載っているものは頂点数が最小で1320なのですが、もっと頂点数の小さい反例はできないか？という問題を学生さんに考えてもらいました。考えてもらった結果、最終的に頂点数115の58次元単体的凸多面体の例が作れ、思った以上に頂点数が小さくなったのでかなり驚きました。見つけてくれた多面体の各次元の面の個数を順番に並べたものがこちら（上から順に、0次元面（頂点）の個数、1次元面（辺）の個数、2次元面の個数、・・・単峰でなくなるところに←を付けています）
115
6555
246905
6913340
153476148
2813729380
43813786060
591486111810
7032112662630
74361634611406
701689496049346
5898793028504600
44040681572082300
291449887676194000
1709790961867370000
8909532023216640000
41372166755718200000
171869015621018000000
641376077739163000000
2158831525832280000000
6579423562008120000000
18220770246145900000000
46000811624755600000000
106184244157205000000000
224700286174916000000000
436963154433157000000000
782625217909075000000000
1293775364438230000000000
1978332674217850000000000
2804826646983420000000000
3697642794754570000000000
4549954481771480000000000
5253976464032560000000000
5737989685641820000000000
5992976271654740000000000
6073851340526980000000000
6071328183931970000000000 ←
6065026796703550000000000 ←
6079130321577480000000000
6063369267661080000000000
5912654196604710000000000
5520348802187850000000000
4840146973252230000000000
3922105289856210000000000
2899955962936760000000000
1935926597911860000000000
1156004422321040000000000
611938502123647000000000
284491105025325000000000
114945469220597000000000
39864229030361000000000
11685085629959300000000
2837245422199600000000
555157567506141000000
84095346673253900000
9252748240613410000
657825579187676000
22683640661644000